The Intersection of Art and Mathematics
Blogs Home
- 03 Apr 2024

Overview
The intersection of logic and beauty, structure and rhythm, symmetry and randomness can be a fine reflection of the connection between mathematics and art. While this connection is as old as civilization itself, a tendency exists to immediately link mathematics to equations, figures, and numbers and rarely to art, music, or architecture. However, it has been discovered that at the core of many masterpieces, melodies, and structures, there are mathematical equations quietly at work. This is easily visible in the art pieces of many musicians, artists, and architects, who knowingly or unknowingly used mathematics for their creations. Let us explore how mathematics impacts art, music, and architecture.
Mathematics and Artworks
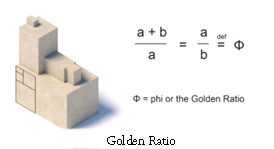
- The Golden Ratio: The golden ratio is a mathematical proportion. It is usually represented by the value φ (phi). It is also known as the divine proportion, represented by a value approximately equal to 1:1.618. To understand it, imagine a large rectangle divided into a series of squares. To find the golden ratio within a rectangle, you divide it into two parts so that the ratio of the longer part to the smaller part is equal to the ratio of the whole length to the longer part. (see figure 1)
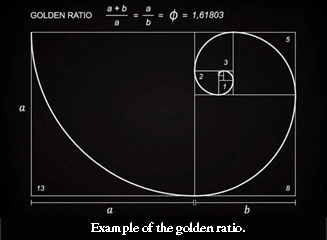
- Artists frequently use this ratio to establish proportions and dimensions in their work to merge aesthetics with a proportional design. Some popular artworks that are believed to have used the proportion, include Leonardo Da Vinci, The Last Supper, 1495-8, Michelangelo, The Creation of Adam, 1508-12, Hokusai, Piet Mondrian, Composition in Red, Yellow, Blue and Black, 1923 and The Great Wave off Kanagawa, 1831 (see figure 2).
- Perspective: Perspective in art is used to create three-dimensional space and objects on a two-dimensional surface. In the process of applying principles of geometry and spatial relationships, artists manipulate lines and vanishing points to create the illusion of depth and volume that draws the viewers into the work and gives a sense of realism.
- There are two primary types of perspective: linear perspective and atmospheric perspective. Linear perspective uses vanishing points and converging lines, whereas atmospheric perspective uses colour and clarity to show depth. A fine example of linear perspective is Leonardo da Vinci's masterpiece "The Last Supper" where the lines of the walls and ceiling converge at a single point behind Christ's head, creating a vanishing point that enhances the sense of depth and distance in the scene, which overall gives a sense of realism and spatial coherence in the work.
- Symmetry: Many artists use symmetry, which is a mathematical concept as a tool to craft visually appealing effects by balancing elements across an axis or multiple axes. It gives a sense of order and balance and creates harmony in art and architecture which are usually categorised as abstract.
- Algorithmic Art: Algorithmic art is a genre wherein algorithms are used to generate patterns and visual effects, to make the work visually striking and elegant. In the early 1960s, alongside advancements in computer technology, the first practices of algorithmic art emerged, as a result of programmable plotter machines.
- These machines, similar to printers, could create continuous line drawings based on commands from a computer. To operate a plotter, users needed to write a program and instruct the machine what to draw, thereby applying the tools of maths, logic, and science. Therefore by using geometric algorithms, artists generated patterns.
 |
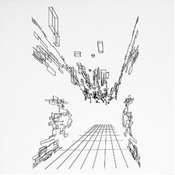 |
Perspectively designed offset lithography graphics from plotter drawings by Georg Nees.
Mathematics and Architecture
Mathematics and architecture have a deep historical connection as well, with mathematicians like Vitruvius and Leonardo da Vinci being architects as well. From site analysis to facade design, mathematics plays an important part at every stage of architectural development and thereby serves both practical and artistic purposes.
- For instance, aids in budgeting as well as determining size, proportions, and spatial divisions within a design. Geometry, symmetry, trigonometry, algebra, and other calculations are used to design the building keeping in mind the environmental considerations like solar radiation intake, wind speeds around, and energy demands of a building.
- This can be observed by looking at ancient temples, mosques, mausoleums, pyramids, and palaces in India, Greece, Egypt, and many other ancient locations.
- The key mathematical concepts that essentially influenced these designs included the Golden Ratio, Fibonacci sequence, and Pi.
The Golden Ratio has been used in structures from Classical Greek temples to Renaissance churches to modern buildings like the Guggenheim Museum in New York City. Similarly, the influence of the Fibonacci sequence, (the sum of the two preceding numbers) can be seen in many architectural classical Greek temples and recent buildings such as Notre-Dame-du-Haut Chapel in France.
Classical mathematics, including Tessellation and Cartesian coordinate systems, offer frameworks for organising space and describing geometric relationships within architecture. Tessellation, which involves repetitive geometric patterns, offers diverse ornamentation possibilities, while Cartesian coordinate systems provide correct spatial representation. While Packing, which is a form of tessellation, addresses density and spatial organisation within architectural compositions the fractional dimensions which came before the decimal system helped in designing the proportional elements in classical architecture. The Cartesian coordinate system, developed by René Descartes, a mathematician revolutionised spatial representation which later facilitated the creation of complex architectural geometries.
Mathematics and Music
Observing the physics of sound, musical notes are vibrations occurring at specific frequencies, and these frequencies are mathematically described by the properties of waves, including their amplitude, frequency, and wavelength.
- String instruments like cellos are carefully designed keeping in mind their shape and size, along with the placement and tension of their strings. In addition, the relationship between notes, intervals, and chords in music can also be understood through mathematical ratios and proportions.
- To take an example, when two notes are played that are a perfect fifth apart, like the C note and G note, the frequency of the higher note, which is ‘G’, is exactly 1.5 times the frequency of the lower note ‘C’, which creates a harmony that is known as a ‘fifth’.
- Interestingly, the golden ratio extended to the realm of music as well, with composers like Bach, Mozart, and Beethoven embedding it within their compositions. The examples of the same can be found in other renowned works such as Bach by Variazioni Goldberg and Beethoven's Symphony No. 5, where the ratio subtly influences the arrangement of accents and the proportions of musical sections.
- Additionally, compositions like Debussy's Preludes and Tool's Lateralus also incorporate the intricate interplay between mathematical principles and music. These pieces serve as crucial examples of how mathematics enriches the fabric of art, architecture as well as musical creation, not only aesthetically but practically as well, and in doing so it infuses within itself both mystery and beauty.
References:
- https://www.cuded.com/exploring-the-intersection-of-mathematics-and-art/
- https://www.thecollector.com/what-is-the-golden-ratio-and-how-does-it-apply-to-art/
- https://www.21-draw.com/what-is-perspective-in-art/?d_currency_code=multi#:~:text=Take%2C%20for%20instance%2C%20Leonardo%20da,a%20convincing%20illusion%20of%20reality.
- https://isfdn.org/balance-symmetry-asymmetry-reference-page/#:~:text=Symmetrical%20balance%20(or%20Symmetry)%20means,however%2C%20try%20to%20create%20balance.
- https://acropolis-greece.com/2023/09/03/the-mathematics-of-the-parthenon/#:~:text=The%20Fibonacci%20Sequence%20is%20a%20mathematical%20pattern%20found,sense%20of%20harmony%20and%20balance%20in%20its%20design.
- https://www.thorarchitects.com/classical-mathematics/
- https://auralcrave.com/en/2020/06/28/the-golden-ratio-in-music-the-songs-of-fibonacci-sequence/?expand_article=1